Im Sommer 2006 ist wieder einmal die Mathematik in den Schlagzeilen
aufgetaucht – sogar die Bildzeitung hat ihr einen Artikel gewidmet: Die
Poincaré-Vermutung war bewiesen. Das begleitende Drama besaß die
meisten Zutaten für einen Bestseller.
Fangen wir aber am besten mit dem Anfang an.
Henri Poincaré
Henri Poincaré hatte seit seinem Schulanfang 1862 in Nancy zielstrebig
seine mathematische Karriere verfolgt und war bis zu seinem Tod
1912 als forschender Mathematiker in Frankreich tätig. Nachdem er sich mit der
Analysis und der Geometrie beschäftigt hatte, publizierte er 1895 den Aufsatz
Analysis Situs: eine der ersten Arbeiten zur algebraischen Topologie.
Seine Arbeiten zur Topologie, welche in den letzten Jahren vor dem
Jahrhundertwechsel entstanden, enthalten unter anderem auch die so genannte Poincaré-Vermutung.
Topologie und Geometrie
Eines der wichtigsten Werkzeuge, die von Poincaré eingeführt wurden,
ist die Fundamentalgruppe eines topologischen Objektes. Um einen Eindruck von dieser
Fundamentalgruppe zu bekommen, betrachten wir zuerst Flächen als spezielle Objekte.
In diese Flächen können wir Schleifen einbetten. Schleifen sind stetige Kurven,
deren Anfangs- und Endpunkt gleich sind und die in einer bestimmten Richtung durchlaufen
werden. Da wir nicht an der genauen Form der Fläche interessiert sind, ist der genaue
Verlauf der Schleife auch nicht von großer Bedeutung. Wir erlauben uns deshalb die
Schleife mittels kleiner stetiger Verschiebungen zu verändern. Dabei muss die Schleife aber
zu jeder Zeit innerhalb der Fläche bleiben und Anfangs- und Endpunkt dürfen nicht verändert
werden. Wenn eine Schleife auf diese Art und Weise in eine andere umgewandelt werden kann,
so nennen wir die beiden Schleifen homotop zueinander. Zwei Schleifen, die homotop
zueinander sind, haben die gleiche Homotopieklasse.
Die Menge der Homotopieklassen bildet mit der beschriebenen Verknüpfung eine Gruppe.
Das neutrale Element ist dabei die Homotopieklasse der konstanten Schleife, die im Anfangspunkt bleibt.
Das inverse Element zu einer Homotopieklasse einer Schleife ist die Klasse der in umgekehrter Richtung durchlaufenen Schleife.
Wir können nun auf der Menge der Homotopieklassen aller Schleifen, die in einem bestimmten
Punkt anfangen, eine Verknüpfung von zwei Schleifen definieren: wir durchlaufen zuerst die
eine und danach die andere Schleife. Wir können zeigen, dass diese Verknüpfung bestimmte
Eigenschaften besitzt (siehe Kasten).
Diese Menge und ihre Verknüpfung bezeichnet man als Fundamentalgruppe.
Sie trägt Informationen über die Fläche. Zum Beispiel ist die Fundamentalgruppe einer Sphäre
trivial, da alle Schleifen, die auf einer Sphäre liegen, sich zu der konstanten Kurve
zusammenziehen lassen – es gibt kein Hindernis und kein Loch, an dem eine Schleife hängen
bleiben könnte.
 Nichttriviale Fundamentalgruppe des Torus
Nichttriviale Fundamentalgruppe des Torus
Auf dem Torus – der Oberfläche eines Rettungsringes oder eines Donuts – dagegen
können wir eine Schleife wie im Bild legen. Wie wir feststellen, lässt sich
diese Kurve, egal wie wir sie verschieben, nicht zusammenziehen. Es zeigt sich, dass es zwei
nicht zusammenziehbare „Grundschleifen” auf dem Torus gibt. Durch Verknüpfungen
dieser beiden Schleifen können wir jede mögliche Homotopieklasse von Schleifen auf dem Torus
erzeugen.
Bei den zweidimensionalen Flächen ohne Rand ist es tatsächlich so, dass die Kenntnis
der Fundamentalgruppe genügt, um die Fläche zu bestimmen. So genügt es zu wissen, dass eine
Fläche kompakt ist und eine triviale Fundamentalgruppe besitzt, um sie als Sphäre zu identifizieren.
Dabei ist eine Fläche kompakt, wenn jede Folge von Punkten der Fläche eine konvergente Teilfolge
besitzt.
Die Vermutung
Für die Verallgemeinerung des Flächenkonzeptes in drei Dimensionen
wird es jedoch sofort viel schwieriger. Diese Verallgemeinerung ist die 3-Mannigfaltigkeit. Das
sind Objekte, die sich in einer Umgebung um jeden Punkt herum wie der Raum
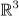 verhalten. (Die Erdoberfläche ist z.B. eine 2-Mannigfaltigkeit –
um jeden Punkt gibt es eine Umgebung, die wie die Ebene aussieht.) Wir können an
jedem Punkt ein dreidimensionales Koordinatensystem für die nähere
Umgebung aufspannen und damit alle lokalen Fragen in Fragen über den Raum
verhalten. (Die Erdoberfläche ist z.B. eine 2-Mannigfaltigkeit –
um jeden Punkt gibt es eine Umgebung, die wie die Ebene aussieht.) Wir können an
jedem Punkt ein dreidimensionales Koordinatensystem für die nähere
Umgebung aufspannen und damit alle lokalen Fragen in Fragen über den Raum
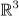 übersetzen. Globale Fragen – z.B. nach der grundlegenden Form der Mannigfaltigkeit
– können wir so nicht beantworten. Wir kennen einige
3-Mannigfaltigkeiten von Interesse:
übersetzen. Globale Fragen – z.B. nach der grundlegenden Form der Mannigfaltigkeit
– können wir so nicht beantworten. Wir kennen einige
3-Mannigfaltigkeiten von Interesse:
-
die 3-Sphäre, definiert als die Menge aller Punkte
(x,y,z,w) ∈
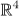 mit
x² + y² + z²: + w² = 1; mit
x² + y² + z²: + w² = 1;
-
der projektive 3-Raum, der aus der 3-Sphäre entsteht, indem jeweils der Punkt
(x,y,z,w) mit dem Punkt (−x,−y,−z,−w)
identifiziert wird; und
-
der 3-Torus, der entsteht, indem man den normalen Torus im vierdimensionalen Raum
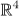 rotiert. rotiert.
Poincaré vermutete, dass sich auch bei den
3-Mannigfaltigkeiten alles so schön verhält wie bei den
Flächen: Wenn die Fundamentalgruppe trivial und die
3-Mannigfaltigkeit genügend „schön” ist, dann handelt es sich um die
3-Sphäre. Diese Vermutung wurde als Poincaré-Vermutung bekannt.
Lösungsversuche
Die Poincaré-Vermutung weckte im Laufe der Jahre langsam das Interesse der Mathematiker
und viele versuchten sie zu beweisen. J. H. C. Whitehead hat in den 1930er Jahren
behauptet, er hätte eine Lösung gefunden, seinen Beweis aber später zurückgezogen. In
den 1950 bis 1960er Jahren wurde eine ganze Reihe von Beweisen aufgestellt
und wieder zurückgezogen. Auch wenn die Beweise öfters gescheitert
sind, haben die für die Beweise entwickelten Methoden durchaus große Fortschritte in der
Topologie bewirkt.
Im Jahre 2000 stellte das Clay Institute sieben Probleme
als so genannte Milleniumsprobleme vor und
sprach für die Lösung jedes dieser Probleme einen Geldpreis von $ 1.000.000 aus. Eines
dieser Probleme war die Poincaré-Vermutung.
William Thurston und die Geometrisierung
William Thurston, der 1982 die Fields-Medaille erhielt, hat sich mit der Geometrie und der
Topologie der 3-Mannigfaltigkeiten beschäftigt. Auf vielen
Mannigfaltigkeiten kann man eine Metrik definieren, das ist ein
Abstandsmaß auf der Oberfläche. Mit Hilfe einer Metrik werden auch mehrere andere Invarianten
definiert, so z.B. die Krümmung.
Hat die Metrik eine konstante positive Krümmung, dann wird sie
sphärisch genannt; hat sie eine konstante negative Krümmung, dann wird sie
hyperbolisch genannt.
Mannigfaltigkeiten, die solche Metriken besitzen, nennen wir sphärisch bzw.
hyperbolisch. Eine dritte Gruppe von
Mannigfaltigkeiten sind die, in welche man einen Torus einbetten kann, diese
heißen torisch. Es lässt sich zeigen, dass hyperbolische und torische
Mannigfaltigkeiten unendliche Fundamentalgruppen und sphärische
Mannigfaltigkeiten endliche Fundamentalgruppen haben. Außerdem können sowohl
in sphärische als auch in hyperbolische
Mannigfaltigkeiten keine Tori eingebettet werden.
Thurston stellte sich die Frage, ob diese drei Klassen von Mannigfaltigkeiten
die einzigen sind. Das heißt, ob eine 3-Mannigfaltigkeit immer entweder sphärisch,
hyperbolisch oder torisch ist. Die größte Frage dabei wäre dann,
ob jede nicht-torische Mannigfaltigkeit mit unendlicher Fundamentalgruppe eine
hyperbolische Metrik zulässt.
Dies wurde für eine Klasse von 3-Mannigfaltigkeiten, die so genannten
Hakenmannigfaltigkeiten, von Thurston gezeigt.
Er vermutete außerdem, dass es auch im allgemeinen Fall nur diese drei Typen gibt.
Diese Vermutung ist als Geometrisierungsvermutung bekannt.
Von der Geometrisierung zu Poincaré
Eine Folge der Geometrisierungsvermutung wäre, dass eine
3-Mannigfaltigkeit mit endlicher Fundamentalgruppe eine sphärische Metrik
zulassen würde. Eine weitere Folge
wäre, dass alle Mannigfaltigkeiten, die hyperbolisch
sein könnten – also eine unendliche Fundamentalgruppe besitzen und nicht torisch sind –
auch hyperbolisch sind. Daher wird es leicht zu erkennen, welche Form eine bestimmte
Mannigfaltigkeit haben kann: sie könnte einen Torus enthalten oder
hyperbolisch sein, beides führt zu einer unendlichen
Fundamentalgruppe; oder sie könnte sphärisch sein und damit eine endliche Fundamentalgruppe besitzen.
Hierdurch stellt sich heraus, dass – falls die Geometrisierungsvermutung
gilt – Mannigfaltigkeiten mit einer endlichen Fundamentalgruppe sphärisch
sind. Unter den sphärischen
Mannigfaltigkeiten wiederum gibt es nur eine mit trivialer Fundamentalgruppe:
die 3-Sphäre.
Richard Hamilton und seine Ricci-Flüsse
Richard Hamilton hat in seinem Studium von sphärischen
3-Mannigfaltigkeiten die Idee der Ricci-Flüsse entwickelt. Er wählte eine
beliebige Metrik mit positiver Krümmung auf der Mannigfaltigkeit aus. Diese Metrik
lässt er dann eine Entwicklung durchlaufen, die durch eine Differentialgleichung – ähnlich
der der Hitzeverbreitung in festen, homogenen Körpern – beschrieben wird. Diese
Entwicklung, genannt der Ricci-Fluss, wird dann alle Unregelmäßigkeiten in
der Krümmung verschmieren, bis man zum Schluss eine Metrik mit
konstanter positiver Krümmung erhält.
Aufgrund seiner Arbeit glaubte Hamilton, dass es möglich sein müsste, die
Geometrisierungsvermutung mit Hilfe
dieser Methode zu beweisen.
Die Vermutung wird bewiesen
Grigori Perelman
Grigori (Grisha) Perelman, ein russischer Mathematiker, der am
Steklov-Institut der Mathematik in Sankt Petersburg tätig war, hat 2002 und 2003 eine Folge von
drei Artikeln im Internet auf dem mathematischen
Artikelserver zur Verfügung gestellt. Diese beschäftigen sich mit dem Thema der
Ricci-Flüsse und zeigen in sehr kurz gefasster Form einige
Eigenschaften dieser Flüsse auf 3-Mannigfaltigkeiten. Vor
allem geben die Arbeiten von Perelman Methoden an, wie man
problematische Regionen aus der 3-Mannigfaltigkeit ausschneiden kann, ohne den Typ
derselben zu verändern. Mit diesen Methoden kann man den Ricci-Fluss ohne Probleme und
innerhalb endlicher Zeit beenden. Dadurch würde jede geeignete Mannigfaltigkeit
eine sphärische Geometrie erhalten können und
die Vermutung von Thurston wäre bewiesen.
Diese Artikel waren aber recht kurz gefasst und skizzenhaft, so dass 2006 verschiedene Gruppen
von Mathematikern – zwei amerikanische
und eine chinesische, eigene Artikel publiziert haben, welche die Arbeit
von Perelman erläutern. So konnten zumindest die Spezialisten in Perelmans Gebiet
den gesamten Beweis nachvollziehen.
Shing-Tung Yau
Die chinesische Gruppe um Professor Shing-Tung Yau –
bekannt unter anderem für die in der Physik wichtigen Calabi-Yau-Mannigfaltigkeiten
– hat dabei ihre Artikel so formuliert, als ob sie den endgültigen
Beweis mit Hilfe von Perelmans Arbeit gefunden hätte. Die Wissenschaftler haben
anerkannt, dass ein Großteil der Arbeit von Perelman durchgeführt
wurde, vertraten aber die Ansicht, dass noch so viel zu einem
vollständigen Beweis zu tun war, dass sie die eigene Arbeit als die
„Krone der Hamilton-Perelmanschen Theorie der Ricci-Flüsse”
bezeichnen dürfen.
Perelman lehnt die Fields-Medaille ab
Seit Perelmans Stelle am Steklov-Institut 2003 nicht verlängert wurde,
hat Perelman sich aus der Welt der Mathematik
zurückgezogen. Er hat in Interviews mit Sylvia Nasar vom New
Yorker gesagt, dass er von den ethischen Standards
der Mathematikerwelt enttäuscht ist und deshalb nichts mehr mit derselben zu tun haben will. Die
Konflikte mit Yau über die Frage, wer eigentlich den letztendlichen
Beweis geleistet habe, sowie Zweifel seiner Kollegen vom
Steklov-Institut an seinen Leistungen haben dazu beigetragen, dass er
sich jetzt abgrenzt.
Zum Internationalen Kongress der Mathematik 2006, wurde Perelman
zusammen mit Terence Tao, Wendelin Werner und Andrei Okounkov die
Fields-Medaille verliehen. Perelman hat die Medaille und den Geldpreis abgelehnt, obwohl ihn der
Präsident der Internationalen Mathematiker-Vereinigung,
Sir John Ball, zwei Tage lang zu überreden versuchte. Perelman meint, dass der Preis nicht
wichtig sei. Falls der Beweis stimmt, sei außerdem keine weitere
Anerkennung nötig.
Die anfangs erwähnten Geldpreise vom Clay-Institut werden vergeben,
wenn der Beweis zwei Jahre nach Veröffentlichung in einer
mathematischen Zeitschrift immer noch als gültig angesehen
wird. Die Artikel von Perelman jedoch wurden nicht in einer
Zeitschrift veröffentlicht, sondern nur auf dem oben genannten Artikelserver.
Falls das Clay-Institut seine Regeln bezüglich der Veröffentlichung lockert und niemand einen
Fehler in Perelmans Beweis findet, könnten Perelman und Hamilton den Preis von $ 1.000.000
angeboten bekommen. Perelman möchte sich jetzt noch nicht entscheiden,
ob er diesen Preis annehmen würde.
Mikael Johansson
|

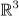 verhalten. (Die Erdoberfläche ist z.B. eine 2-Mannigfaltigkeit –
um jeden Punkt gibt es eine Umgebung, die wie die Ebene aussieht.) Wir können an
jedem Punkt ein dreidimensionales Koordinatensystem für die nähere
Umgebung aufspannen und damit alle lokalen Fragen in Fragen über den Raum
verhalten. (Die Erdoberfläche ist z.B. eine 2-Mannigfaltigkeit –
um jeden Punkt gibt es eine Umgebung, die wie die Ebene aussieht.) Wir können an
jedem Punkt ein dreidimensionales Koordinatensystem für die nähere
Umgebung aufspannen und damit alle lokalen Fragen in Fragen über den Raum
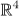 mit
x² + y² + z²: + w² = 1;
mit
x² + y² + z²: + w² = 1;