Aufgabe 1
Die Hypotenuse eines rechtwinkliges Dreiecks beträgt 4cm.
Das Dreieck wird um die Hypotenuse gedreht.
Ermittle das größtmögliche Volumen des entstandenen Drehkörpers.
Lösung
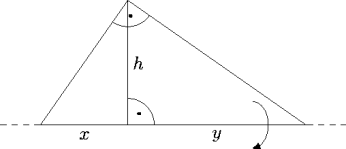 Es entstehen zwei senkrechte Kreiskegel mit dem gemeinsamen Radius h
und den Höhen x und y (siehe Figur).
Damit ist das Gesamtvolumen
Es entstehen zwei senkrechte Kreiskegel mit dem gemeinsamen Radius h
und den Höhen x und y (siehe Figur).
Damit ist das Gesamtvolumen
V = 1/3·π·h2·x
+ 1/3·π·h2·y
= 1/3·π·h2·(x + y)
= 1/3·π·h2·4
oder
V(h) = 4π/3·h2
Dieses Volumen soll maximal werden.
V'(h)= 8π/3·h
Die erste Ableitung muss Null sein.
V'(h) = 0
⇔ 8π/3·h = 0
⇔ h = 0
⇒ Vmax = V(0) = 0
Das maximale Volumen kann aber unmöglich Null sein.
Widerspruch! – Was ist richtig? Was ist falsch? Warum?
Einführung und weitere Aufgaben
|
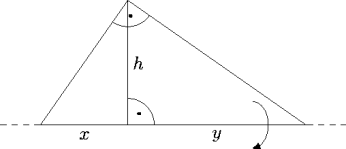 Es entstehen zwei senkrechte Kreiskegel mit dem gemeinsamen Radius h
und den Höhen x und y (siehe Figur).
Damit ist das Gesamtvolumen
Es entstehen zwei senkrechte Kreiskegel mit dem gemeinsamen Radius h
und den Höhen x und y (siehe Figur).
Damit ist das Gesamtvolumen